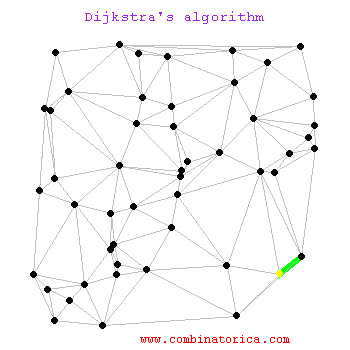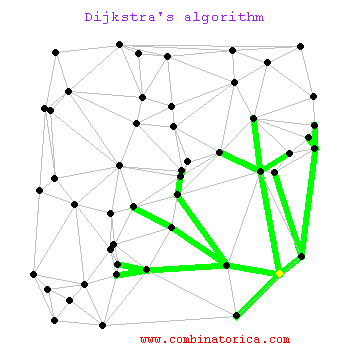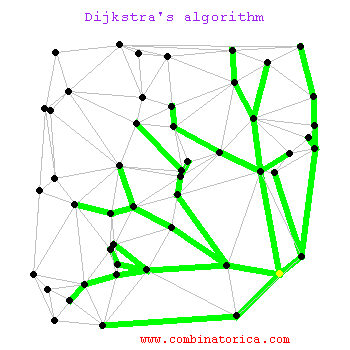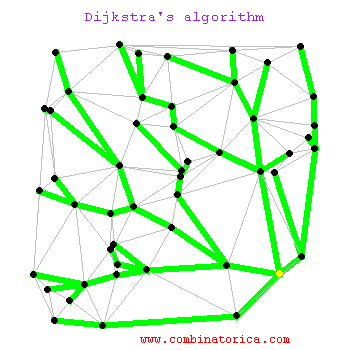
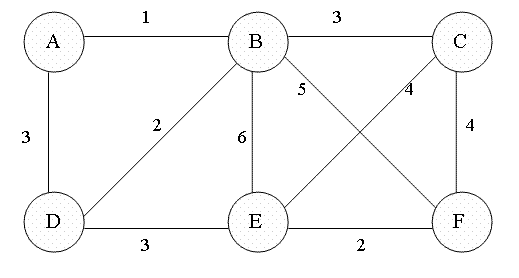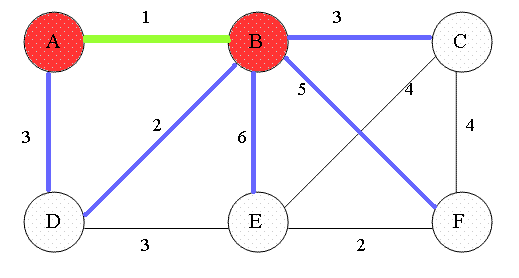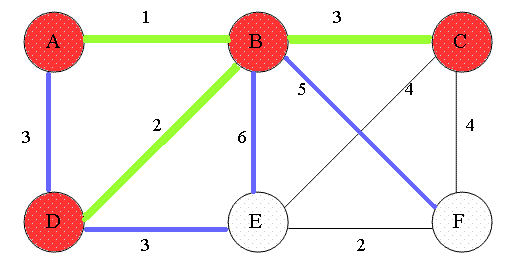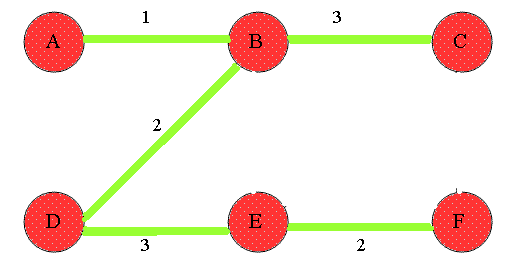
最短路径算法

Dijkstra

伟大，无需多言。实际上Dijkstra算法就是维护了一个dist数组，定义dist[i]表示起点到i号节点的最短距离值。这样，从起点出发，更新当前邻居节点的距离。由于在初始化dist数组时会将除起点外所有节点设置为不可达(INT_MAX)，因此每次更新dist数组时，最小的距离一定是可达的。

每次更新dist数组，即寻找当前距离最小的节点，然后遍历其邻居节点。

方程为：

1
2
3
4
if (dist[node] + weight < dist[neighbor]) {
    dist[neighbor] = dist[node] + weight;  
    pq.push({dist[neighbor], neighbor}); 
}

这里可以看到使用了优先队列(本质上是二叉最小堆)来优化Dijkstra算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <iostream>
#include <vector>
#include <queue>
#include <limits>
using std::cout;
using std::cin;
using std::pair;
using std::vector;
using std::priority_queue;
using std::endl;

typedef pair<int, int> pii; // 定义一个pair类型的别名pii，用于表示图中的节点号和边权
const int INF = INT_MAX; // 定义一个表示无穷大的常量INF，用于初始化距离数组

// Dijkstra算法实现，计算从start到end的最短路径距离
int dijkstra(const vector<vector<pii>>& graph, int n, int start, int end) {
    vector<int> dist(n + 1, INF); // 初始化距离数组，表示从start到每个节点的最短距离，默认为无穷大
    dist[start] = 0; // 设置起始节点到自身的距离为0，因为距离自身的距离为0

    // 使用最小堆实现优先队列，存储节点和距离的pair，按距离从小到大排序
    // 队列中的元素是 (距离, 节点) 对
    priority_queue<pii, vector<pii>, std::greater<pii>> pq;
    pq.push({0, start}); // 将起始节点和距离0加入优先队列

    // 开始Dijkstra算法的主循环，直到优先队列为空
    while (!pq.empty()) {
        int d = pq.top().first; // 当前节点到起始节点的距离
        int node = pq.top().second; // 当前节点的编号
        pq.pop(); // 弹出队首元素

        if (d > dist[node])
            continue; // 如果当前节点到起始节点的距离大于已知的最短距离，则跳过

        // 遍历当前节点的所有邻居节点
        for (auto& edge : graph[node]) {
            int neighbor = edge.first; // 邻居节点的编号
            int weight = edge.second; // 边的权重

            // 如果通过当前节点到达邻居节点的距离比已知的最短距离小，则更新距离数组，并将邻居节点加入优先队列
            if (dist[node] + weight < dist[neighbor]) {
                dist[neighbor] = dist[node] + weight; // 更新最短距离
                pq.push({dist[neighbor], neighbor}); // 将邻居节点和新的最短距离加入优先队列
            }
        }
    }

    // 如果终点的最短距离仍然是无穷大，表示无法到达终点，返回-1；否则返回最短距离
    if (dist[end] == INF) {
        return -1;
    } else {
        return dist[end];
    }
}

int main() {
    int n, m;

    cin >> n >> m; // 输入节点数和边数
    vector<vector<pii>> graph(n + 1); // 创建邻接表，存储图的边和权重

    // 输入图的边和权重信息
    for (int i = 0; i < m; i++) {
        int x, y, z;
        cin >> x >> y >> z;
        graph[x].push_back({y, z}); // 将边(x, y)和权重z加入邻接表
    }

    // 计算从节点1到节点n的最短路径距离，并输出结果
    int shortest_distance = dijkstra(graph, n, 1, n);
    cout << shortest_distance << endl;
    return 0;
}

dijkstra

img

Bellman-Ford

Dijkstra无法解决有负权边的图，需要使用Bellman-Ford算法每次对每个边进行遍历，判断是否有更优路径。这个操作被称为松弛操作，即判断d[u]+length[u->v] < d[v]。如果为真，则d[u]+length[u->v]覆盖d[v]。松弛操作最多为V-1次，也就是节点数减一。松弛操作的次数也代表路径边数可能的最大值。时间复杂度为$\mathcal{O}(VE)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <iostream>
#include <vector>
#include <climits>
#include <utility>
using namespace std;

typedef pair<int, int> pii; // 定义边的结构体，其中 first 表示目标节点，second 表示边的权重

const int INF = INT_MAX; // 定义无穷大

// Bellman-Ford算法实现，计算从起点到终点的最短路径距离
int bellmanFord(const vector<vector<pii>>& graph, int n, int start, int end, int k) {
    vector<int> dist(n + 1, INF); // 存储起点到每个节点的最短距离，初始值为无穷大

    dist[start] = 0; // 起点到自身的距离为0

    // 进行k次松弛操作
    for (int i = 0; i < k; ++i) {
        vector<int> temp = dist; // 备份当前最短距离
        // 遍历每个节点
        for (int u = 1; u <= n; ++u) {
            // 遍历当前节点的所有邻居边
            for (const pii& edge : graph[u]) {
                int v = edge.first; // 邻居节点编号
                int weight = edge.second; // 边的权重
                // 如果起点到当前边的起点的距离不为无穷大，并且经过当前边到达终点的距离比终点原来的距离小，则更新终点的距离
                if (dist[u] != INF && dist[u] + weight < temp[v]) {
                    temp[v] = dist[u] + weight;
                }
            }
        }
        dist = temp; // 更新最短距离数组
    }

    if (dist[end] == INF) { // 如果终点的距离仍为无穷大，则表示无法到达
        return INF;
    } else {
        return dist[end]; // 返回从起点到终点的最短距离
    }
}

int main() {
    int n, m, k;
    // 输入节点数、边数、限制条件k
    cin >> n >> m >> k;

    vector<vector<pii>> graph(n + 1); // 创建邻接表，存储图的边和权重
    // 输入每条边的起点、终点和权重，将边添加到邻接表中
    for (int i = 0; i < m; ++i) {
        int x, y, z;
        cin >> x >> y >> z;
        graph[x].push_back({y, z});
    }

    int ans = bellmanFord(graph, n, 1, n, k); // 调用Bellman-Ford算法计算最短距离

    if (ans == INF) { // 如果最短距离为无穷大，则输出"impossible"
        cout << "impossible" << endl;
    } else {
        cout << ans << endl; // 输出最短距离
    }

    return 0;
}

img

SPFA

Bellman-Ford算法的思路很简洁，但是时间复杂度为$\mathcal{O}(VE)$，很容易超时。因为其每轮操作都需要遍历所有的边，注定有大量重复的无意义操作。SPFA便是维护一个队列对Bellman-Ford算法进行优化，一般的时间复杂度为$\mathcal{O}(kE)$。当图中有源点可达的负环时退化为$\mathcal{O}(VE)$​

优化的思路是：只有当某个顶点u的d[u]值改变时，从它出发的边的邻接点v的d[v]值才有可能被改变。通过维护一个队列，每次将队首顶点u取出，遍历所有边u->v进行松弛操作，如果d[u]+length[u->v] < d[v]，则d[u]+length[u->v]覆盖d[v]，此时如果v不在队列中，则将v加入队列。循环直到队列为空。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
#include <utility>
using namespace std;

typedef pair<int, int> pii; // 定义边的结构体，其中 first 表示目标节点，second 表示边的权重

const int INF = INT_MAX; // 定义无穷大

int spfa(const vector<vector<pii>>& graph, int n, int start, int end) {
    vector<int> dist(n + 1, INF); // 存储起点到每个节点的最短距离，初始值为无穷大
    vector<bool> inQueue(n + 1, false); // 记录节点是否在队列中
    queue<int> q; // 使用队列进行松弛操作

    dist[start] = 0; // 起点到自身的距离为0
    q.push(start); // 将起点加入队列
    inQueue[start] = true; // 标记起点已在队列中

    while (!q.empty()) {
        int u = q.front();
        q.pop();
        inQueue[u] = false; // 标记节点u已出队列

        // 遍历节点u的所有邻居边
        for (const pii& edge : graph[u]) {
            int v = edge.first; // 邻居节点编号
            int weight = edge.second; // 边的权重

            // 如果起点到节点u的距离加上边权重小于起点到节点v的距离，则更新节点v的距离并将其加入队列
            if (dist[u] + weight < dist[v]) {
                dist[v] = dist[u] + weight;
                if (!inQueue[v]) { // 如果节点v不在队列中，则将其加入队列
                    q.push(v);
                    inQueue[v] = true;
                }
            }
        }
    }

    return dist[end]; // 返回从起点到终点的最短距离
}

int main() {
    int n, m;
    cin >> n >> m; // 输入节点数和边数

    vector<vector<pii>> graph(n + 1); // 创建邻接表，存储图的边和权重
    // 输入每条边的起点、终点和权重，将边添加到邻接表中
    for (int i = 0; i < m; ++i) {
        int x, y, z;
        cin >> x >> y >> z;
        graph[x].push_back({y, z});
    }

    int ans = spfa(graph, n, 1, n); // 调用SPFA算法计算最短距离

    if (ans == INF) { // 如果最短距离为无穷大，则输出"impossible"
        cout << "impossible" << endl;
    } else {
        cout << ans << endl; // 输出最短距离
    }

    return 0;
}

image-20200921211548307.png

img

Floyd

Floyd算法用于解决全源最短路径问题。其时间复杂度为$\mathcal{O}(V^3)$

很显然图的顶点数V不可能过大（一般不超过200），因此可以使用邻接矩阵而非邻接表来存储图。

Floyd的思想类似Bellman-Ford的松弛操作，即：

如果存在顶点k，使得以k作为从i到j途径的中介点时可以缩短后两者的当前最短路径距离，则使用k来更新i到j的路径。也就是：

1
2
if (distance[i][k]+dis[k][j] < distance[i][j])
    distance[i][j] = distance[i][k] + distance[k][j];
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

const int INF = 1e9; // 定义一个足够大的数代表无穷大

int main() {
    int n, m, k;
    cin >> n >> m >> k;

    vector<vector<int>> dist(n, vector<int>(n, INF));

    // 初始化自环为0
    for (int i = 0; i < n; i++) {
        dist[i][i] = 0;
    }

    // 读取边信息，更新距离
    for (int i = 0; i < m; i++) {
        int x, y, z;
        cin >> x >> y >> z;
        x--; y--; // 将1-based索引转为0-based索引
        dist[x][y] = min(dist[x][y], z); // 考虑重边，保留最短的那条边
    }

    // Floyd-Warshall算法
    for (int k = 0; k < n; k++) { // k为中间节点
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (dist[i][k] < INF && dist[k][j] < INF) {
                    dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
                }
            }
        }
    }

    // 处理询问
    for (int i = 0; i < k; i++) {
        int x, y;
        cin >> x >> y;
        x--; y--; // 将1-based索引转为0-based索引
        if (dist[x][y] == INF) {
            cout << "impossible" << endl;
        } else {
            cout << dist[x][y] << endl;
        }
    }

    return 0;
}

MST

Prim

Prim实质上是一种贪心的算法，从一个给定起点出发，每次遍历自身邻居，找到当前最短路径的点，延伸生成树。适用于稠密图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <iostream>
#include <vector>
#include <queue>
#include <climits>

using namespace std;

struct Edge {
    int v, w;
    Edge(int _v, int _w) : v(_v), w(_w) {}
};

int main() {
    int n, m;
    cin >> n >> m;

    vector<vector<Edge>> graph(n + 1);
    for (int i = 0; i < m; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        graph[u].emplace_back(v, w);
        graph[v].emplace_back(u, w); // 如果是无向图，需要双向加边
    }

    vector<bool> visited(n + 1, false);
    vector<int> minCost(n + 1, INT_MAX);

    // 使用优先队列保存候选边，按照边的权重进行排序
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;

    int start = 1; // 选择任意一个节点作为起点
    minCost[start] = 0; // 起点到自身的距离为0
    pq.push({0, start}); // 将起点加入优先队列

    int totalCost = 0; // 最小生成树的总权值

    while (!pq.empty()) {
        int u = pq.top().second;
        int minDist = pq.top().first;
        pq.pop();

        if (visited[u]) continue;
        visited[u] = true;

        totalCost += minDist;

        for (const Edge& e : graph[u]) {
            int v = e.v;
            int w = e.w;
            if (!visited[v] && w < minCost[v]) {
                minCost[v] = w;
                pq.push({w, v});
            }
        }
    }

    // 判断是否所有节点都已经加入了最小生成树
    bool possible = true;
    for (int i = 1; i <= n; ++i) {
        if (!visited[i]) {
            possible = false;
            break;
        }
    }

    if (possible) cout << totalCost << endl;
    else cout << "impossible" << endl;

    return 0;
}

img

Kruscal

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

struct Edge {
    int u, v, w;
    bool operator<(const Edge& other) const {
        return w < other.w;
    }
};

vector<int> parent;

int find(int x) {
    return parent[x] == x ? x : parent[x] = find(parent[x]);
}

void unite(int x, int y) {
    parent[find(x)] = find(y);
}

int main() {
    int n, m;
    cin >> n >> m;
    vector<Edge> edges(m);
    for (int i = 0; i < m; ++i) {
        cin >> edges[i].u >> edges[i].v >> edges[i].w;
    }

    sort(edges.begin(), edges.end());

    parent.resize(n + 1);
    for (int i = 1; i <= n; ++i) {
        parent[i] = i;
    }

    int count = 0;
    int sum = 0;
    for (const auto& e : edges) {
        if (find(e.u) != find(e.v)) {
            unite(e.u, e.v);
            sum += e.w;
            ++count;
        }
    }

    if (count == n - 1) {
        cout << sum << endl;
    } else {
        cout << "impossible" << endl;
    }

    return 0;
}

File:Kruskal algorithm.gif

File:MST kruskal en.gif

Bipartite Graph

Staining

染色法判定二分图实际上是对图的每个未染色的点进行一次BFS，将起始节点染成一种颜色，入队；遍历队列，每次取出队首顶点，检查其所有邻接顶点：

  • 如果未染色，则染成不同的颜色并入队
  • 如果已染色并且颜色与邻接顶点相同，则该图不是二分图，否则继续检查下一个顶点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <iostream>
#include <vector>
#include <queue>

using namespace std;

const int N = 1e5 + 10;  // 假设最大的顶点数为 100000
vector<int> G[N];        // 存储图的邻接表
int color[N];            // 存储每个顶点的颜色，0 表示未染色，1 和 -1 表示两种不同的颜色

// 判断图是否为二分图的函数
bool isBipartite(int n) {
    for (int i = 1; i <= n; ++i) {
        if (color[i] == 0) {  // 如果当前节点未染色
            queue<int> q;
            q.push(i);
            color[i] = 1;  // 将起始节点染色为 1

            while (!q.empty()) {
                int u = q.front();
                q.pop();

                for (int v : G[u]) {
                    if (color[v] == 0) {  // 如果相邻节点未染色，则染成不同的颜色
                        color[v] = -color[u];
                        q.push(v);
                    } else if (color[v] == color[u]) {  // 如果相邻节点颜色相同，则不是二分图
                        return false;
                    }
                }
            }
        }
    }
    return true;  // 如果所有节点都能满足条件，则是二分图
}

int main() {
    int n, m;
    cin >> n >> m;

    for (int i = 0; i < m; ++i) {
        int u, v;
        cin >> u >> v;
        G[u].push_back(v);  // 将边加入图中
        G[v].push_back(u);  // 无向图，所以需要双向添加
    }

    cout << (isBipartite(n) ? "Yes" : "No") << endl;

    return 0;
}

Hungary algorithm

匈牙利算法用于求解二分图的最大匹配数。与染色法不同，该算法是基于DFS的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <iostream>
#include <vector>
#include <cstring>

using namespace std;

const int N = 1e3 + 10;  // 假设左右两边顶点数的最大值

vector<int> G[N];    // 存储图的邻接表
int match[N];        // 存储右侧点集中的点与左侧点集中的点的匹配情况
bool used[N];        // 标记数组，用于DFS中标记右侧点集中的点是否被访问过

// DFS函数尝试对左侧点u进行匹配
bool dfs(int u) {
    for (int v : G[u]) {
        if (!used[v]) {
            used[v] = true;  // 标记点v为已访问
            // 如果点v未被匹配或者v已匹配的点可以找到其他匹配
            if (match[v] == 0 || dfs(match[v])) {
                match[v] = u;  // 将点v与点u匹配
                return true;
            }
        }
    }
    return false;
}

// 求二分图的最大匹配数
int bipartiteMatching(int n1, int n2) {
    int result = 0;
    memset(match, 0, sizeof(match));
    for (int i = 1; i <= n1; ++i) {
        memset(used, 0, sizeof(used));
        if (dfs(i)) {
            ++result;  // 如果找到增广路径，匹配数加1
        }
    }
    return result;
}

int main() {
    int n1, n2, m;
    cin >> n1 >> n2 >> m;

    for (int i = 0; i < m; ++i) {
        int u, v;
        cin >> u >> v;
        G[u].push_back(v);
    }

    cout << bipartiteMatching(n1, n2) << endl;

    return 0;
}