哈希

1. 两数之和

使用unordered_map创建一个哈希表，对于数值num，查找是否存在target-num，返回对应的索引

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> umap;
        vector<int> ans;
        for (int i = 0; i < nums.size(); i++) {
            if (umap.count(target - nums[i]) && (umap[target - nums[i]] != i)) {
                ans.push_back(umap[target - nums[i]]);
                ans.push_back(i);
                break;
            }
            umap[nums[i]] = i;
        }
        return ans;
    }
};

49. 字母异位词分组

组合字母组成相同的单词，编译原理写过类似的题，可以先将所有单词按照字典序排序，然后创建哈希表即可。

128. 最长连续序列

可以使用unordered_set，对其中的每个数字判断其前驱数num-1是否在哈希表中，如果不在，则其是一个新的序列，重新计数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <vector>
#include <unordered_set>
#include <algorithm>

class Solution {
public:
    int longestConsecutive(std::vector<int>& nums) {
        // 如果输入数组为空，则最长连续序列的长度为0
        if (nums.empty()) return 0;

        // 将所有数字插入到一个哈希集合中，以去除重复元素并加快查找速度
        std::unordered_set<int> num_set(nums.begin(), nums.end());

        // 初始化最长连续序列的长度
        int longest_streak = 0;

        // 遍历哈希集合中的每个数字
        for (int num : num_set) {
            // 如果当前数字的前驱数字不在集合中，说明它是一个新的序列的起点
            if (!num_set.count(num - 1)) {
                // 初始化当前连续序列的起点
                int current_num = num;
                // 初始化当前连续序列的长度
                int current_streak = 1;

                // 检查当前数字的后继数字是否存在于集合中
                while (num_set.count(current_num + 1)) {
                    // 如果存在，延长当前序列并增加序列长度
                    current_num += 1;
                    current_streak += 1;
                }

                // 更新最长连续序列的长度
                longest_streak = std::max(longest_streak, current_streak);
            }
        }

        // 返回最长连续序列的长度
        return longest_streak;
    }
};

滑动窗口

3. Longesst substring without repeating characters

这道题的解法很巧妙：使用unordered_set维护一个窗口，使用双指针遍历字符串，如果窗口中存在当前字符，说明有重复字符，则移动左指针直到无重复字符，然后右指针继续向右移动，每次移动都会更新答案，保持答案为窗口最大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int left = 0, n = s.length(), ans = 0;
        unordered_set<char> window;

        for (int right = 0; right < n; right++) {
            char c = s[right];
            while (window.count(c)) {
                window.erase(s[left]);
                left++;
            }

            window.insert(c);
            ans = max(ans, right - left + 1);
        }
        return ans;
    }
};

只需要遍历一次数组，时间复杂度为$\mathcal{O}(n)$​​

438. Find All Anagrams in a String

很自然地想到哈希表，因为本质上是要找到pattern中各个字母各自出现的次数在原字符中的对应起始下标

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<int> findAnagrams(string s, string p) {
        vector<int> result, hash(26, 0);
        int ls = s.length(), lp = p.length();
        for (int i = 0; i < lp; i++) {
            hash[p[i] - 'a']++;
        }

        for (int i = 0; i <= ls - lp; i++) {
            vector<int> tempHash(26, 0);
            for (int j = i; j < i + lp; j++) {
                tempHash[s[j] - 'a']++;
            }
            if (tempHash == hash) {
                result.push_back(i);
            }
        }
        return result;
    }
};

滑动窗口

上述操作虽然逻辑简洁，但是时间复杂度为$\mathcal{O}(mn)$，有很多冗余操作。可以参考KMP算法来保存前面的判断结果。提高算法效率：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    vector<int> findAnagrams(string s, string p) {
        vector<int> result, hashP(26, 0), window(26, 0);
        int ls = s.length(), lp = p.length();
        
        if (ls < lp) return result; // s 比 p 短时直接返回空结果
        
        // 统计 p 的字符频率
        // 先在window窗口中添加s和p的前lp个字符
        for (int i = 0; i < lp; i++) {
            hashP[p[i] - 'a']++;
            window[s[i] - 'a']++;
        }

        // 比较初始窗口和 p 的字符频率
        if (window == hashP) result.push_back(0);

        // 滑动窗口
        // 窗口逐步向右移动，判断是否仍然与
        for (int i = lp; i < ls; i++) {
            // 移除左端字符，添加右端字符
            window[s[i - lp] - 'a']--;
            window[s[i] - 'a']++;
            
            // 比较当前窗口和 p 的字符频率
            if (window == hashP) result.push_back(i - lp + 1);
        }
        
        return result;
    }
};

很重要的一点是：

vector重载了比较运算符 == 和 !=。这些运算符允许我们直接比较两个 std::vector 对象是否相等或不等。当我们使用 == 运算符比较两个 std::vector 时，实际进行的是元素逐个比较，只有当两个向量的大小相同并且对应位置的元素都相等时，比较结果才为 true。

560. Subarray sum = k

哈希表+前缀和，基础模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<int, int> prefixSumCount; // 哈希表存储前缀和及其出现次数
        prefixSumCount[0] = 1; // 初始化前缀和为0的情况
        
        int currentSum = 0;
        int result = 0;
        
        for (int num : nums) {
            currentSum += num; // 计算当前前缀和
            
            // 检查是否存在前缀和，使得 currentSum - k = 之前的某个前缀和
            if (prefixSumCount.count(currentSum - k)) {
                result += prefixSumCount[currentSum - k];
            }
            
            // 更新哈希表中当前前缀和的出现次数
            prefixSumCount[currentSum]++;
        }
        
        return result;
    }
};

239. Sliding Windows Maximum

使用双端队列存储数组元素的索引，然后维护此队列成为单调队列，front处为最大值，每次弹出队列中小于当前元素的元素和超出窗口尺寸的元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        deque<int> deq;  // 双端队列，存储数组元素的索引
        vector<int> ans; // 存储结果
        
        for (int i = 0; i < nums.size(); ++i) {
            // 移除队列中所有不在当前窗口范围内的元素
            if (!deq.empty() && deq.front() == i - k) {
                deq.pop_front();
            }
            
            // 移除队列中所有小于当前元素 nums[i] 的元素
            while (!deq.empty() && nums[deq.back()] < nums[i]) {
                deq.pop_back();
            }
            
            // 将当前元素的索引 i 添加到队列的尾部
            deq.push_back(i);
            
            // 如果窗口已经形成，添加当前窗口的最大值到结果数组
            if (i >= k - 1) {
                ans.push_back(nums[deq.front()]);
            }
        }
        
        return ans;
    }
};

双指针

283. 移动零

没想到的思路：初始化一个非零位置的lastNonZeroFoundAt指针表示此位置之前的元素全部非0，然后遍历数组：如果当前位置元素不为0，则将此元素移动至非零指针处，然后lastNonZeroFoundAt指针向前移动。在移动非零元素后，如果lastNonZeroFoundAt指针与当前索引不一致，说明发生了元素移动，则将i的位置填充0，表示移位。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    void moveZeroes(std::vector<int>& nums) {
        // 初始化非零元素放置位置指针
        int lastNonZeroFoundAt = 0;

        // 遍历数组
        for (int i = 0; i < nums.size(); i++) {
            // 如果当前元素不是0
            if (nums[i] != 0) {
                // 将当前元素移动到 lastNonZeroFoundAt 指针所在位置
                nums[lastNonZeroFoundAt] = nums[i];
                // 如果 i 不等于 lastNonZeroFoundAt，说明发生了移动
                if (i != lastNonZeroFoundAt) {
                    nums[i] = 0; // 将当前位置填充为0
                }
                // 移动 lastNonZeroFoundAt 指针到下一个位置
                lastNonZeroFoundAt++;
            }
        }
    }
};

11. 盛最多水的容器

暴力搜索是每次都从当前指针出发遍历数组，时间复杂度为$\mathcal{O}^2$，通过了55/62个样例，超时。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int maxArea(vector<int>& height) {
        int maxWater = 0;
        for (int i = 0; i < height.size(); i++) {
            for (int j = i + 1; j < height.size(); j++) {
                int currentWater = 0;
                currentWater = min(height[i], height[j]) * (j - i);
                maxWater = max(currentWater, maxWater);
            }
        }

        return maxWater;
    }
};

使用双指针优化，可以先设置位于数组两端的指针，然后每次移动较低的容器，找到最大值，直到两指针相遇：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    int maxArea(std::vector<int>& height) {
        // 初始化左右指针
        int left = 0;
        int right = height.size() - 1;
        // 初始化最大面积
        int maxWater = 0;

        // 当左指针小于右指针时进行循环
        while (left < right) {
            // 计算当前容器的高度和宽度
            int currentHeight = std::min(height[left], height[right]);
            int currentWidth = right - left;
            // 计算当前容器的面积
            int currentWater = currentHeight * currentWidth;
            // 更新最大面积
            maxWater = std::max(maxWater, currentWater);

            // 移动较小高度的指针以尝试找到更大的面积
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }

        return maxWater;
    }
};

15. 三数之和

双指针解法

先对数组排序方便指针查找，然后固定第一个指针。如果当前位置的元素与上一位置元素相同，则跳过以避免重复判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        // 排序数组
        sort(nums.begin(), nums.end());
        vector<vector<int>> result;

        // 遍历数组，固定第一个元素
        for (int i = 0; i < nums.size(); i++) {
            // 如果当前元素与上一个元素相同，跳过以避免重复
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }

            // 使用双指针寻找另外两个元素
            int left = i + 1;
            int right = nums.size() - 1;

            while (left < right) {
                int sum = nums[i] + nums[left] + nums[right];
                if (sum == 0) {
                    // 找到满足条件的三元组，加入结果集
                    result.push_back({nums[i], nums[left], nums[right]});

                    // 移动左指针跳过重复元素
                    while (left < right && nums[left] == nums[left + 1]) {
                        left++;
                    }
                    // 移动右指针跳过重复元素
                    while (left < right && nums[right] == nums[right - 1]) {
                        right--;
                    }

                    // 移动指针寻找下一组元素
                    left++;
                    right--;
                } else if (sum < 0) {
                    // 如果和小于0，移动左指针以增加总和
                    left++;
                } else {
                    // 如果和大于0，移动右指针以减小总和
                    right--;
                }
            }
        }

        return result;
    }
};

精简代码

0x3f的解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    vector<vector<int>> threeSum(vector<int> &nums) {
        sort(nums.begin(), nums.end());
        vector<vector<int>> ans;
        int n = nums.size();
        for (int i = 0; i < n - 2; ++i) {
            int x = nums[i];
            if (i && x == nums[i - 1]) continue; // 跳过重复数字
            if (x + nums[i + 1] + nums[i + 2] > 0) break; // 优化一
            if (x + nums[n - 2] + nums[n - 1] < 0) continue; // 优化二
            int j = i + 1, k = n - 1;
            while (j < k) {
                int s = x + nums[j] + nums[k];
                if (s > 0) --k;
                else if (s < 0) ++j;
                else {
                    ans.push_back({x, nums[j], nums[k]});
                    for (++j; j < k && nums[j] == nums[j - 1]; ++j); // 跳过重复数字
                    for (--k; k > j && nums[k] == nums[k + 1]; --k); // 跳过重复数字
                }
            }
        }
        return ans;
    }
};

/*
作者：灵茶山艾府
链接：https://leetcode.cn/problems/3sum/solutions/1968332/shuang-zhi-zhen-xiang-bu-ming-bai-yi-ge-pno55/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
*/

42. 接雨水

双指针解法

双指针方法：维护两个指针从两端向中间扫描，并记录每个位置的最大高度来计算雨水量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    int trap(vector<int>& height) {
        if (height.empty()) return 0;

        // 设置左右指针
        int left = 0, right = height.size() - 1;
        int leftMax = 0, rightMax = 0;
        int waterTrapped = 0;

        while (left < right) {
            // 如果左边的高度小于右边的高度，则处理左边
            if (height[left] < height[right]) {
                // 当前高度大于或等于左边最大高度，更新左边最大高度
                // 否则计算当前高度能够接住的水量
                if (height[left] >= leftMax) {
                    leftMax = height[left];
                } else {
                    waterTrapped += leftMax - height[left];
                }
                left++;
            } else {
                // 右侧同理
                if (height[right] >= rightMax) {
                    rightMax = height[right];
                } else {
                    waterTrapped += rightMax - height[right];
                }
                right--;
            }
        }

        return waterTrapped;
    }
};

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    int trap(vector<int>& height) {
        if (height.empty()) return 0;

        int n = height.size();
        vector<int> leftMax(n), rightMax(n);
        leftMax[0] = height[0];
        rightMax[n - 1] = height[n - 1];

        // 计算每个位置左边的最大高度
        for (int i = 1; i < n; i++) {
            leftMax[i] = max(leftMax[i - 1], height[i]);
        }

        // 计算每个位置右边的最大高度
        for (int i = n - 2; i >= 0; i--) {
            rightMax[i] = max(rightMax[i + 1], height[i]);
        }

        int waterTrapped = 0;
        // 计算每个位置能够接住的水量
        for (int i = 0; i < n; i++) {
            waterTrapped += min(leftMax[i], rightMax[i]) - height[i];
        }

        return waterTrapped;
    }
};

单调栈

1

滑动窗口

3. 最长重复子串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int left = 0, n = s.length(), ans = 0;
        unordered_set<char> window;
        for (int right = 0; right < n; right++) {
            char c = s[right];
            while (window.count(c)) {
                window.erase(s[left++]);
            }
            window.insert(c); // 加入 c
            ans = max(ans, right - left + 1); // 更新窗口长度最大值
        }
        return ans;
    }
};

链表

160. 相交链表

用了一个unordered_set作为节点的哈希表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution
{
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB)
    {
        ListNode* ptrA = headA;
        ListNode* ptrB = headB;
        unordered_set<ListNode*> uset;
        ListNode* ans = NULL;
        while (ptrA) {
            if (uset.count(ptrA)) {
                ptrA = ptrA->next;
                continue;
            }
            uset.insert(ptrA);
            ptrA = ptrA->next;
        }
        while (ptrB) {
            if (uset.count(ptrB)) {
                ans = ptrB;
                return ans;
            }
            ptrB = ptrB->next;
        }
        return ans;
    }
};

206. 反转链表

来自柳神的解法，我的原想法是开辟一个栈自然实现倒序，柳神是直接在内部交换指针的指向关系，非常妙

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if (head == NULL) return head;

        ListNode* curr = head, *prev = NULL, *temp = NULL;
        while (curr) {
            temp = curr->next;
            curr->next = prev;
            prev = curr;
            curr = temp;
        }
        return prev;
    }
};

234. 回文链表

还是用栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    bool isPalindrome(ListNode* head) {
        stack<ListNode*> stk;
        ListNode* nptr = head;
        while (nptr) {
            stk.push(nptr);
            nptr = nptr->next;
        }
        nptr = head;
        while (!stk.empty()) {
            if (stk.top()->val == nptr->val) {
                stk.pop();
                nptr = nptr->next;
            } else {
                return false;
            }
        }
        return true;
    }
};

141. 环形链表

unordered_set

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode* nptr = head;
        if (nptr == NULL || nptr->next == NULL) return false;
        unordered_set<ListNode*> uset;
        while (nptr) {
            if (uset.count(nptr)) return true;
            uset.insert(nptr);
            nptr = nptr->next;
        }
        return false;
    }
};

142. 环形链表II

这样的空间复杂度为$\mathcal{O}(n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* nptr = head;
        ListNode* ans = NULL;
        unordered_set<ListNode*> uset;
        int i = 0;
        while (nptr) {
            if (uset.count(nptr)) {
                return nptr;
            }
            uset.insert(nptr);
            nptr = nptr->next;
        }
        
        return ans;
    }
};

柳神的代码类似：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if (head == NULL) return NULL;
        unordered_set<ListNode*> uset;
        ListNode *p = head;
        int cnt = 0;
        while (p->next) {
            uset.insert(p);
            if (cnt == uset.size()) return p;
            cnt = uset.size();
            p = p->next;
        }
        return NULL;
    }
};

快慢指针

官方题解提供了一个快慢指针的思路，可以将空间复杂度优化到$\mathcal{O}(1)$​。

在链表上有两个移速不同的指针，如果这两个指针能够相遇，则一定存在环，这是检测是否有环的经典算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode *slow = head, *fast = head;
        while (fast != nullptr) {
            slow = slow->next;
            if (fast->next == nullptr) {
                return nullptr;
            }
            fast = fast->next->next;
            if (fast == slow) {
                ListNode *ptr = head;
                while (ptr != slow) {
                    ptr = ptr->next;
                    slow = slow->next;
                }
                return ptr;
            }
        }
        return nullptr;
    }
};

21. 合并两个有序链表

实际上是多个分类处理。首先声明一个表头，然后遍历两个链表：当一个链表上的节点的值较小时，加入答案链表，然后将这个链表上的指针后移。当有链表达到尾端时，另一个链表余下的部分直接加入链表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        ListNode* dum = new ListNode(0);
        ListNode* cur = dum;
        while (list1 != nullptr && list2 != nullptr) {
            if (list1->val < list2->val) {
                cur->next = list1;
                list1 = list1->next;
            }
            else {
                cur->next = list2;
                list2 = list2->next;
            }
            cur = cur->next;
        }
        cur->next = list1 != nullptr ? list1 : list2;
        return dum->next;
    }
};

2. 两数之和

使用链表倒序存储两数，一步步进位得到两数之和，思路不难，主要是模拟平时的加法计算过程，大概用于大数求和：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        int carry = 0;
        ListNode* head = new ListNode(0);
        ListNode* nptr = head;

        while (l1 != nullptr || l2 != nullptr || carry != 0) {
            int value = carry;
            if (l1 != nullptr) {
                value += l1->val;
                l1 = l1->next;
            }
            if (l2 != nullptr) {
                value += l2->val;
                l2 = l2->next;
            }

            carry = value / 10;
            nptr->next = new ListNode(value % 10);
            nptr = nptr->next;
        }

        return head->next; // 返回结果链表的头节点（去除初始化的0节点）
    }
};

19. 删除链表的倒数第 N 个节点

我的原代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        if (!head || !head->next) return nullptr;
        if (n == 1) {
            ListNode* ptr = head;
            while (ptr->next) {
                ptr = ptr->next;
            }
            ptr->next = nullptr;
            delete ptr->next;
            return head;
        }
        ListNode* fptr = head;
        ListNode* sptr = head;
        for (int i = 0; i < n; i++) {
            sptr = sptr->next;
        }
        while (sptr->next) {
            fptr = fptr->next;
            sptr = sptr->next;
        }

        fptr->next = sptr;
        return head;
    }

可以看到无法处理n超出链表长度的情况以及删除操作存在逻辑错误。

改进代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        // 创建一个哑节点，指向头节点，处理边界情况
        ListNode* dummy = new ListNode(0);
        dummy->next = head;
        ListNode* first = dummy;
        ListNode* second = dummy;

        // 让 second 指针先走 n+1 步
        for (int i = 0; i <= n; ++i) {
            if (second == nullptr) return head; // n 超过链表长度
            second = second->next;
        }

        // 移动 first 和 second 指针直到 second 指向链表末尾
        while (second != nullptr) {
            first = first->next;
            second = second->next;
        }

        // 删除第 n 个节点
        ListNode* nodeToDelete = first->next;
        first->next = first->next->next;
        delete nodeToDelete;

        // 返回处理后的链表头节点
        ListNode* newHead = dummy->next;
        delete dummy; // 释放哑节点内存
        return newHead;
    }
};

创建dummy节点简化边界处理，实际上就是数据结构课里的不带值的头结点。然后让second指针走n+1步，这样才能正确删除节点，也就是两节点中间隔了一个节点。注意后面的while语句中的判断条件是second != nullptr，这样second节点实际上走到了尾节点的后一节点的位置，也就是空值处，这时删除的节点正是倒数第N个节点。

24. Swap Nodes in Pairs

主要是对链表各节点的next进行操作，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if (!head || !head->next) return head;

        ListNode* dummy = new ListNode(0);
        dummy->next = head;
        ListNode* prev = dummy;

        while (prev->next && prev->next->next) {
            ListNode* first = prev->next;
            ListNode* second = prev->next->next;

            first->next = second->next;
            second->next = first;
            prev->next = second;
            prev = first;
        }

        ListNode* newHead = dummy->next;
        delete dummy;
        return newHead;
    }
};

递归

递归的代码非常简短，但是不容易理解。可以从栈顶的情况开始分析：当只有一个元素时，不再递归，直接返回当前链表。由于我们创建的变量为newHead = head->next，而传入的参数是newHead->next，那么返回的便是head->next->next。由交换的示意图可以得知，head->next = head->next->next。最后，表头的两节点交换：newHead->next = head;

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if (!head || !head->next) return head;

        ListNode* newHead = head->next;
        head->next = swapPairs(newHead->next);
        newHead->next = head;
        return newHead;
    }
};

迭代

在循环中，程序检查当前节点temp及其后面是否有足够的两个节点进行交换。如果有，则进行节点交换操作。

  • node1指向当前节点的下一个节点，即第一个要交换的节点。
  • node2指向node1的下一个节点，即第二个要交换的节点。
  • 然后，程序进行节点交换操作：
    • 将temp的next指针指向node2，实现交换。
    • 将node1的next指针指向node2的下一个节点，连接后续节点。
    • 将node2的next指针指向node1，完成节点交换。
  • 最后，将temp移动到下一组要交换的节点的前一个节点，继续循环直到链表末尾或无法再进行交换。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public ListNode swapPairs(ListNode head) {
        ListNode dummyHead = new ListNode(0);
        dummyHead.next = head;
        ListNode temp = dummyHead;
        while (temp.next != null && temp.next.next != null) {
            ListNode node1 = temp.next;
            ListNode node2 = temp.next.next;
            temp.next = node2;
            node1.next = node2.next;
            node2.next = node1;
            temp = node1;
        }
        return dummyHead.next;
    }
}

25. Reverse Nodes in k-Group

类似24：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        if (!head || k == 1) return head;

        ListNode* dummy = new ListNode(0);
        dummy->next = head;
        ListNode* prev = dummy;

        int count = 0;
        while (head) {
            count++;
            if (count % k == 0) {
                prev = reverse(prev, head->next);
                head = prev->next;
            } else {
                head = head->next;
            }
        }

        ListNode* newHead = dummy->next;
        delete dummy;
        return newHead;
    }
private:
    ListNode* reverse(ListNode* prev, ListNode* next) {
        ListNode* last = prev->next;
        ListNode* current = last->next;
        while (current != next) {
            last->next = current->next;
            current->next = prev->next;
            prev->next = current;
            current = last->next;
        }
        return last;
    }
};

递归

三个指针current、prev和nextNode，分别表示当前节点、前一个节点和下一个节点。然后利用循环将每k个节点进行翻转操作。翻转操作就是将当前节点的next指针指向前一个节点，然后更新prev和current指针。

翻转完成后，head节点指向翻转后的最后一个节点，prev指针指向翻转后的头节点。接下来，程序使用递归调用自身来翻转下一个k个节点，并将翻转后的头节点连接到翻转前的尾部。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        if (!head || k == 1) {
            return head;
        }

        ListNode* nextGroupHead = head;
        for (int i = 0; i < k; i++) {
            if (!nextGroupHead) {
                return head; // 如果长度不够k，直接返回头节点
            }
            nextGroupHead = nextGroupHead->next;
        }

        ListNode* current = head;
        ListNode* prev = nullptr;
        for (int i = 0; i < k; i++) {
            ListNode* nextNode = current->next;
            current->next = prev;
            prev = current;
            current = nextNode;
        }

        head->next = reverseKGroup(nextGroupHead, k); // 将翻转后的头节点连接下一个k的头节点
        return prev; // 返回翻转后的头节点
    }
};

138. Copy List with Random Pointer

回溯+哈希

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    unordered_map<Node*, Node*> cachedNode;

    Node* copyRandomList(Node* head) {
        if (head == nullptr) {
            return nullptr;
        }
        if (!cachedNode.count(head)) {
            Node* headNew = new Node(head->val);
            cachedNode[head] = headNew;
            headNew->next = copyRandomList(head->next);
            headNew->random = copyRandomList(head->random);
        }
        return cachedNode[head];
    }
};

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
class Solution {
public:
    Node* copyRandomList(Node* head) {
        if (!head) {
            return nullptr; // If the input list is empty, return nullptr.
        }
        /*
            Original List:
            1 -> 2 -> 3 -> null
            |    |    |
            v    v    v
            2   null  1
        */

        // First pass: Create a new node for each existing node and interleave them.
        // 遍历原始链表，对于每个节点，创建一个新节点并将其插入到原节点之后
        /*
            After interleaving:
            1 -> 1' -> 2 -> 2' -> 3 -> 3' -> null
            |          |          |
            v          v          v
            2         null        1
        */
        for (Node* current = head; current != nullptr;) {
            Node* newNode = new Node(current->val);
            newNode->next = current->next;
            current->next = newNode;
            current = newNode->next;
        }

        // Second pass: Assign random pointers for the new nodes.
        // 为新节点设置随机指针
        /*
            Interleaved list with `random` pointers set:
            1 -> 1' -> 2 -> 2' -> 3 -> 3' -> null
            |    |     |    |     |    |
            v    v     v    v     v    v
            2    2'   null null   1    1'
        */
        for (Node* current = head; current != nullptr; current = current->next->next) {
            if (current->random != nullptr) {
                current->next->random = current->random->next;
            }
        }

        // Third pass: Separate the original list from the copied list and prepare the return value.
        // 将原始链表和复制链表分开，并恢复原始链表的结构。
        /*
            Restored original list:
            1 -> 2 -> 3 -> null
            |    |    |
            v    v    v
            2   null  1

            Separated copied list (deep copy):
            1' -> 2' -> 3' -> null
            |     |     |
            v     v     v
            2'   null   1'
        */
        Node* copiedListHead = head->next;
        for (Node* current = head; current != nullptr;) {
            Node* copiedNode = current->next;
            // Advance the current pointer in the original list to the next original node
            current->next = copiedNode->next;
            // Advance the copiedNode pointer in the copied list to the next copied node, 
            // if it exists
            if (copiedNode->next != nullptr) {
                copiedNode->next = copiedNode->next->next;
            }
            // Move to the next original node
            current = current->next;
        }

        // Return the head of the copied list.
        return copiedListHead;
    }
};

时间复杂度：对链表做了3次遍历，为$\mathcal{O}(N)$；空间复杂度：实用的额外空间是常数级，为$\mathcal{O}(1)$​

148. Sort List

自定义一个lambda表达式（类似重载比较符），然后维护一个最小堆自动排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    ListNode* sortList(ListNode* head) {
        auto cmp = [](const ListNode& a, const ListNode& b) {
            return a.val > b.val; // 根据 val 的值从大到小排序
        };

        priority_queue<ListNode, vector<ListNode>, decltype(cmp)> pq(cmp);
        ListNode* curr = head;
        while (curr) {
            pq.push(*curr);
            curr = curr->next;
        }

        ListNode dummy(0);
        ListNode* tail = &dummy;
        while (!pq.empty()) {
            tail->next = new ListNode(pq.top().val);
            pq.pop();
            tail = tail->next;
        }

        return dummy.next;

    }
};

归并排序

递归调用sort函数来进行归并排序：即每次将链表均分为两段，然后对各个halves进行分类，最后合并每个有序链表：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
public:
    ListNode* sortList(ListNode* head) {
        // Base case: if the list is empty or has only one element, it is already sorted.
        if (!head || !head->next) return head;

        // Use the fast and slow pointer approach to find the middle of the list
        ListNode* slow = head;
        ListNode* fast = head->next;
        while (fast && fast->next) {
            slow = slow->next;
            fast = fast->next->next;
        }

        // Split the list into two halves
        ListNode* midNext = slow->next;
        slow->next = nullptr;
      
        // Recursively sort both halves
        ListNode* leftHalf = sortList(head);
        ListNode* rightHalf = sortList(midNext);
      
        // Merge the two sorted halves
        ListNode* dummyHead = new ListNode();
        ListNode* current = dummyHead;
        while (leftHalf && rightHalf) {
            // Choose the smaller value from either half
            if (leftHalf->val <= rightHalf->val) {
                current->next = leftHalf;
                leftHalf = leftHalf->next;
            } else {
                current->next = rightHalf;
                rightHalf = rightHalf->next;
            }
            // Move to the next node in the merged list
            current = current->next;
        }
      
        // If there are remaining nodes in either half, append them to the merged list
        current->next = leftHalf ? leftHalf : rightHalf;
      
        // The merged sorted list is pointed to by the dummy head's next node
        ListNode* sortedHead = dummyHead->next;
        delete dummyHead; // Clean up the dummy node
        return sortedHead;
    }
};

时间复杂度为$\mathcal{O}(n\log n)$​

23. Merge K sorted lists

优先队列就是神

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution
{
public:
    ListNode *mergeKLists(vector<ListNode *> &lists)
    {
        // Lambda function to compare two ListNode pointers for the min-heap
        auto cmp = [](ListNode *a, ListNode *b)
        { return a->val > b->val; };

        // Priority queue (min-heap) to keep track of the smallest element
        priority_queue<ListNode *, vector<ListNode *>, decltype(cmp)> minHeap(cmp);

        // Insert the first node of each list into the heap
        for (auto list : lists)
        {
            if (list)
            {
                minHeap.push(list);
            }
        }

        // Dummy head to ease the merging process
        ListNode dummy;
        ListNode *current = &dummy;

        while (!minHeap.empty())
        {
            // Extract the smallest node from the heap
            ListNode *minNode = minHeap.top();
            minHeap.pop();

            // Add the smallest node to the merged list
            current->next = minNode;
            current = current->next;

            // If the extracted node has a next node, insert it into the heap
            if (minNode->next)
            {
                minHeap.push(minNode->next);
            }
        }

        return dummy.next; // Return the head of the merged list
    }
};

146. LRU Cache

实际就是手动实现双线链表+哈希表：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
class Node {
public:
    int key, value;
    Node* prev;
    Node* next;

    Node(int k = 0, int v = 0) : key(k), value(v) {}
};


class LRUCache {
private:
    int capacity;
    Node *dummy; // 哨兵节点
    unordered_map<int, Node*> key_to_node;

    // 删除一个节点（抽出一本书）
    void remove(Node *x) {
        x->prev->next = x->next;
        x->next->prev = x->prev;
    }

    // 在链表头添加一个节点（把一本书放在最上面）
    void push_front(Node *x) {
        x->prev = dummy;
        x->next = dummy->next;
        x->prev->next = x;
        x->next->prev = x;
    }

    Node *get_node(int key) {
        auto it = key_to_node.find(key);
        if (it == key_to_node.end()) // 没有这本书
            return nullptr;
        auto node = it->second; // 有这本书
        remove(node); // 把这本书抽出来
        push_front(node); // 放在最上面
        return node;
    }

public:
    LRUCache(int capacity) : capacity(capacity), dummy(new Node()) {
        dummy->prev = dummy;
        dummy->next = dummy;
    }

    int get(int key) {
        auto node = get_node(key);
        return node ? node->value : -1;
    }

    void put(int key, int value) {
        auto node = get_node(key);
        if (node) { // 有这本书
            node->value = value; // 更新 value
            return;
        }
        key_to_node[key] = node = new Node(key, value); // 新书
        push_front(node); // 放在最上面
        if (key_to_node.size() > capacity) { // 书太多了
            auto back_node = dummy->prev;
            key_to_node.erase(back_node->key);
            remove(back_node); // 去掉最后一本书
            delete back_node; // 释放内存
        }
    }
};

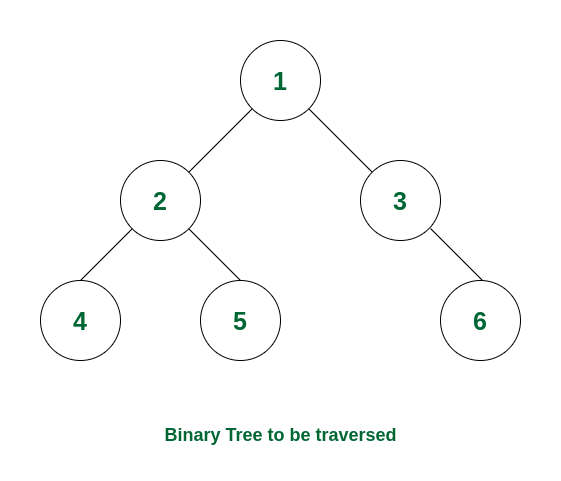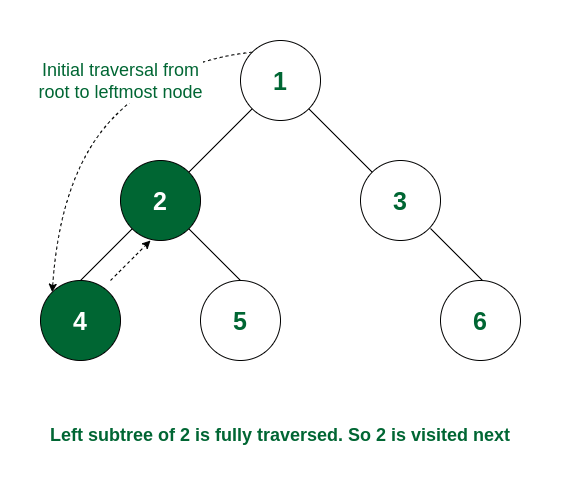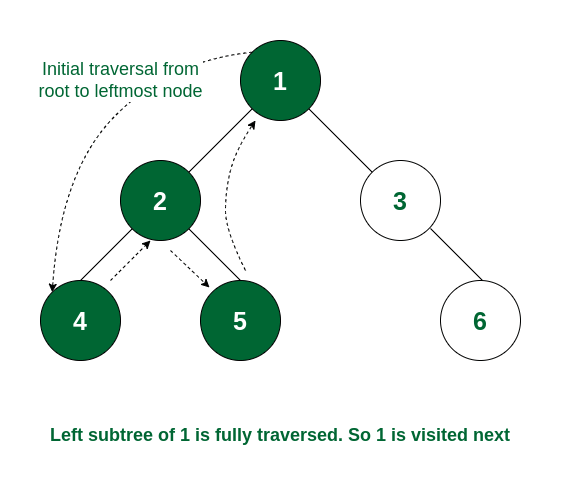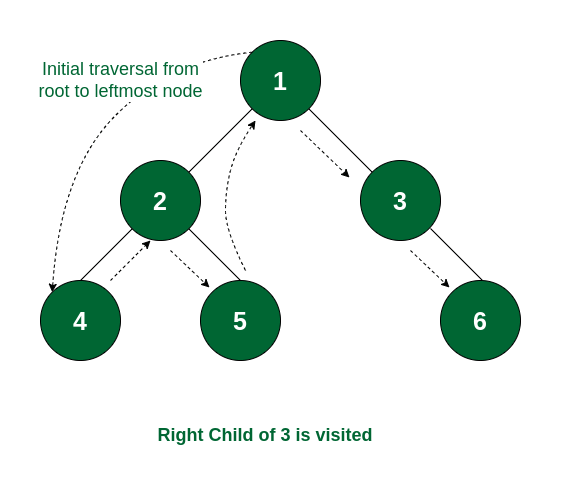
二叉树

94. Binary tree inorder traversal

拆解中序遍历的过程：

  1. The left subtree is traversed first
  2. Then the root node for that subtree is traversed
  3. Finally, the right subtree is traversed

递归

直接左中右：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    void inorder(TreeNode* root, vector<int>& ans) {
        if (!root) {
            return;
        }

        inorder(root->left, ans);
        ans.push_back(root->val);
        inorder(root->right, ans);
    }
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;
        inorder(root, ans);
        return ans;
    }

};

迭代

中序遍历的过程：

inorder

将递归写法改为迭代，实际就是使用栈来模拟递归调用的函数栈。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;
        stack<TreeNode*> stk;
        TreeNode* curr = root;
        while (curr || !stk.empty()) {
            if (curr) {
                stk.push(curr);
                // 先一直沿着左子树方向移动
                curr = curr->left;
            } else {
                // 找到最后被遍历的节点，就是其自己的根节点。
                curr = stk.top();
                stk.pop();
                ans.push_back(curr->val);
                // 因为左子树已经被遍历完了
                // 寻找右子树
                curr = curr->right;
            }
        }
        return ans;
    }

};

104. Maximum depth of binary tree

不停地向左子树和右子树递归，更新向左或向右的最大深度，实际上是一个dfs。

1
2
3
4
5
6
7
8
9
class Solution {
public:
    int maxDepth(TreeNode *root) {
        if (root == nullptr) return 0;
        int l_depth = maxDepth(root->left);
        int r_depth = maxDepth(root->right);
        return max(l_depth, r_depth) + 1;
    }
}

迭代

维护一个队列，从根节点root开始，每次遍历队列中所有节点（通过开始时候的队列大小获取节点个数），然后push进所有节点的所有子节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int maxDepth(TreeNode* root) {
        queue<TreeNode*> q;
        int depth = 0;
        if (!root) return depth;

        q.push(root);
        while (!q.empty()) {
            int n = q.size();
            depth++;
            for (int i = 0; i < n; i++) {
                TreeNode* node = q.front();
                q.pop();
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
        }
        return depth;
    }
};

递归

使用了模板，这里实际上是一个Inorder Traversal，每次遍历将当前深度+1，二维vector的result中对应下标的vector即为对应层次的所有节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    void order(TreeNode* cur, vector<vector<int>>& result, int depth) {
        if (cur == nullptr) return;
        if (result.size() == depth) result.push_back(vector<int>());
        result[depth].push_back(cur->val);
        order(cur->left, result, depth + 1);
        order(cur->right, result, depth + 1);
    }
    int maxDepth(TreeNode* root) {
        vector<vector<int>> result;
        int depth = 0;
        order(root, result, depth);
        return result.size();
    }
};

226. Invert binary tree

很容易想到递归

递归

对每个节点的left child和right child，递归调用函数，最后交换左右：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (!root) return NULL;

        TreeNode* left = invertTree(root->left);
        TreeNode* right = invertTree(root->right);

        root->right = left;
        root->left = right;

        return root;
    }
};

时间和空间复杂度都是$\mathcal{O}(n)$

迭代

使用一个栈来辅助遍历二叉树节点，对于遇到的每一个节点，交换左右子节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (!root) return NULL;
        stack<TreeNode*> stk;
        stk.push(root);
        while (!stk.empty()) {
            TreeNode* curr = stk.top();
            stk.pop();

            // 交换当前节点的左右子节点
            TreeNode* temp = curr->left;
            curr->left = curr->right;
            curr->right = temp;

            // 将子节点加入栈中
            if (curr->left) {
                stk.push(curr->left);
            }
            if (curr->right) {
                stk.push(curr->right);
            }
        }
        return root;
    }
};

101. Symmetric tree

递归

这个也很自然地想到递归解法，实际上是对树做了一个遍历，但是不能按照left child和right child来判断，而是要按照“外侧”和“里侧”来分类。也就是根的左子树要等于根的右子树，左子树的右子树要等于右子树的左子树，也就是里侧相等，外侧相等。

体现完整逻辑的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    bool compare(TreeNode* left, TreeNode* right) {
        if (left == nullptr && right != nullptr) {
            return false;
        } else if (left != nullptr && right == nullptr) {
            return false;
        } else if (left == nullptr && right == nullptr) {
            return true;
        } else if (left->val != right->val) {
            return false;
        }

        bool outside = compare(left->left, right->right);
        bool inside = compare(left->right, right->left);
        bool isSame = outside && inside;
        return isSame;
    }
    bool isSymmetric(TreeNode* root) {
        if (!root) return true;
        return compare(root->left, root->right);
    }
};

精简后为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    bool compare(TreeNode* left, TreeNode* right) {
        if (left == NULL && right != NULL) return false;
        else if (left != NULL && right == NULL) return false;
        else if (left == NULL && right == NULL) return true;
        else if (left->val != right->val) return false;
        else return compare(left->left, right->right) && compare(left->right, right->left);

    }
    bool isSymmetric(TreeNode* root) {
        if (root == NULL) return true;
        return compare(root->left, root->right);
    }
};

迭代

维护一个队列，判空后，每次判断一对节点是否相等，在加入队列时也两两成对加入队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
bool isSymmetric(TreeNode* root) {
        if (root == NULL) return true;

        queue<TreeNode*> q;
        q.push(root->left);
        q.push(root->right);

        while (!q.empty()) {
            TreeNode* left = q.front();
            q.pop();
            TreeNode* right = q.front();
            q.pop();

            if (!left && !right) continue;  // 左右节点都为空，对称，继续检查
            if (!left || !right) return false;  // 一个为空，一个不为空，不对称
            if (left->val != right->val) return false;  // 两个节点值不相等，不对称

            // 将子节点按对称顺序加入队列
            q.push(left->left);
            q.push(right->right);
            q.push(left->right);
            q.push(right->left);
        }

        return true;
    }

实际上改用栈也完全可以：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (!root) return true;

        stack<TreeNode*> stk;
        stk.push(root->left);
        stk.push(root->right);

        while (!stk.empty()) {
            TreeNode* left = stk.top();
            stk.pop();
            TreeNode* right = stk.top();
            stk.pop();

            if (!left && !right) {
                continue;
            }

            if (!left || !right || left->val != right->val) {
                return false;
            }

            stk.push(left->left);
            stk.push(right->right);
            stk.push(left->right);
            stk.push(right->left);
        }
        return true;
    }
};

杂记

unordered_map&set

unordered_map is an associative container that contains key-value pairs with unique keys. Search, insertion, and removal of elements have average constant-time complexity. Internally, the elements are not sorted in any particular order, but organized into buckets. Which bucket an element is placed into depends entirely on the hash of its key.

可以看到unordered_map的内部实现是hash，而map的内部是红黑树，这也就是是否“unordered”的区别，二者的各项操作的平均时间复杂度分别为$\mathcal{O}(1)$和$\mathcal{O}(\log_2 N)$​。map的迭代效率更高而unordered_map的操作效率更高。

dummy node

A linked list implementation may use a dummy node (or header node): A node with an unused data member that always resides at the head of the list and cannot be removed. Using a dummy node simplifies the algorithms for a linked list because the head and tail pointers are never null. An empty list consists of the dummy node, which has the next pointer set to null, and the list’s head and tail pointers both point to the dummy node. Singly-linked lists with and without a dummy node.

priority_queue

The priority queue) is a container adaptor that provides constant time lookup of the largest (by default) element, at the expense of logarithmic insertion and extraction.

A user-provided Compare can be supplied to change the ordering, e.g. using std::greater would cause the smallest element to appear as the top().

priority_queue实际维护了一个有序堆，通过greater<T>或less<T>（默认）分别设定为最小堆和最大堆，即越小的元素越靠近堆顶或越大的元素越靠近堆顶。