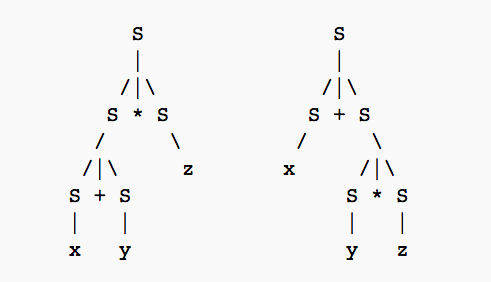SKI Combinator Calculus

Basic Elements

Combinator:

A function without free variables

Calculus:

A method of computation or calculation in a special notation

Something about combinator

Combinator

The SKI combinator calculus is a combinatory logic system and a computational system.

All operations in lambda calculus can be encoded via abstraction elimination into the SKI calculus as binary trees whose leaves are one of the three symbols S, K, and I (called combinators).

$S$ takes two funtions $f$ and $g$, returns a new funtion, which apply input to each of $f$ and $g$, then combine them. $S$ is a way to program function calls (applications) and reuse values (make copies).

This rule is called Generalized funtion application.

$S\ x\ y\ z\rightarrow(x\ z)\ (y\ z)$

or more intuitively but less generally which means apply $x$ to funtion $f$ and $g$:

$S\ f\ g\ x \rightarrow (f\ x)\ (g\ x)$

Definition of $S$ combinator in lambda calculus:

$S=\lambda f.\lambda g.\lambda x.(f\ x)\ (g\ x)$

$K$ takes two parameter and return the first one. It’s called Constant functions

$K\ x\ y\rightarrow x$

Defined in lambda calculus:

$K=\lambda x.\lambda y.x$

The simplest one is $I$, return what it gets. Indentity function

$I\ x\rightarrow x$

In lambda calculus:

$I=\lambda x.x$

Definition Rules

The terms of the SKI calculus are the smallest set such that\

$S$, $K$, and $I$ are terms
If $x$ and $y$ are terms, then $x\ y$ is a term

Terms are trees, not strings

Parentheses show association where necessary
In the absence of parentheses, association is to the left
- i.e., $S\ x\ y\ z=(((S\ x)\ y)\ z)$

     S    
   /   \
  K     \
 / \     \
K   x     \
           S
          / 
         y

或

       /\
      /  \
     /    \
    /\     \
   /  \    /\
  /    \  S  y
 /\    /\
S  K  K  x

Grammar

Context Free Grammar:

$\begin{aligned} & \text{Expr}\rightarrow S\\ & \text{Expr}\rightarrow K\\ & \text{Expr}\rightarrow I\\ & \text{Expr}\rightarrow \text{Expr Expr}\\ & \text{Expr}\rightarrow \text{(Expr)} \end{aligned}$ $\text{Expr}\rightarrow S\ |\ K\ |\ I\ |\ \text{Expr Expr}\ |\ \text{(Expr)}$

A context-free grammar is a set of recursive rules used to generate patterns of strings. A context-free grammar can describe all regular languages and more, but they cannot describe all possible languages.

wiki

Take “x+y*z” as example:

x+y*z

In particular, in a context-free grammar, each production rule is of the form $A\rightarrow\alpha$ with $A$ a single nonterminal symbol, and $\alpha$ a string of terminals and/or nonterminals ($\alpha$ can be empty). Regardless of which symbols surround it, the single nonterminal A on the left hand side can always be replaced by $\alpha$ on the right hand side.

🤖（ChatGPT）：

上下文无关文法中，每个产生式的左侧是单一的非终结符，而右侧可以是终结符或非终结符的任意组合。

在 SKI 组合子计算中，上下文无关文法可以用来描述组合子的有效表达式（即组合子表达式）。

这些规则定义了一个名为 $Expr$ 的非终结符，它表示 SKI 组合子计算中的合法表达式。每一条规则都是一个产生式，描述了如何从一些符号（终结符或非终结符）构造一个有效的表达式。下面逐条解释这些规则。

Expr → S

这个规则表示表达式 $Expr$ 可以是 $S$ 组合子。也就是说，$S$ 是一个合法的表达式。

Expr → K

这个规则表示表达式 $Expr$ 可以是 $K$ 组合子。即 $K$ 是一个合法的表达式。

Expr → I

这个规则表示表达式 $Expr$ 可以是 $I$ 组合子。即 $I$ 是一个合法的表达式。

Expr → Expr Expr

这个规则表示表达式 $Expr$ 可以由两个表达式组合而成。两个 $Expr$ 表达式通过空格（表示函数应用）连接起来。例如，如果 $E1$ 和 $E2$ 是两个有效的 $Expr$，那么 $E1\ E2$ 也是一个有效的表达式。这个规则定义了函数应用的基本结构。换句话说，它表示两个组合子表达式可以组合成一个更复杂的表达式。

例如，$S\ K$ 表示 $S$ 应用 $K$，是一个合法的 $Expr$。

Expr → (Expr)

这个规则表示表达式 $Expr$ 可以被括号括起来，这允许表达式可以嵌套。在某些情况下，括号有助于明确表达式的优先级或结构。

例如，$S\ K$ 是一个合法的表达式，表示将 $S$ 应用到 $K$。

综合来看：

这些规则定义了 SKI 组合子计算中的所有可能的表达式的结构。$S$、$K$ 和 $I$ 是基本的终结符，可以直接作为表达式；而 $Expr\ Expr$ 和 $(Expr)$`$ 则提供了表达式的组合方式和结构。

通过这些规则，任何合法的 SKI 组合子表达式都可以通过组合这些基本规则生成。例如：

$S$

$K$

$I$

$S\ K$

$S\ K$

$S\ (K\ I)$

$(S\ K)\ I$

$S\ S\ (K\ I)$

这些都是符合给定文法的合法表达式。这种文法是上下文无关的，因为规则的应用不依赖于上下文（例如，位置或其他符号的状态），而是只依赖于当前的符号（在这个例子中是 $Expr$）。

Rewrite Rules

The three rules of the SKI calculus are an example of a rewrite system

Any expression (or subexpression) that matches the left-hand side of a rule can be replaced by the right-hand side

The symbol $\rightarrow$ stands for a single rewrite

The symbol $\rightarrow^*$ stands for the reflexive, transitive closure of $\rightarrow$

$S\ K\ x\ y\rightarrow(K\ y)\ (x\ y)\rightarrow y$

Recursion

$\begin{align} S\ I\ I\ x \\ &\hspace{-2em} \rightarrow (I\ x)\ (I\ x) \\ &\hspace{-2em} \rightarrow x\ (I\ x) \\ &\hspace{-2em} \rightarrow x\ x \end{align}$

Noticed it’s self-calling:

$\begin{aligned} (S\ I\ I)\ (S\ I\ I)\\ &\hspace{-4em}\rightarrow (I\ (S\ I\ I)\ (I\ (S\ I\ I))\\ &\hspace{-4em}\rightarrow (S\ I\ I)\ (I\ (S\ I\ I))\\ &\hspace{-4em}\rightarrow (S\ I\ I)\ (S\ I\ I) \end{aligned}$

Can always be rewritten, since it rewrites to itself

A form of looping

Condition

Encoding:

We choose combinators to represent $\text{true}$, $\text{false}$
And combinators $\text{not}$, $\text{or}$, $\text{and}$ that have the correct behavior on those values

Abstract Data Type (ADT)

Except there is no type system to enforce the abstractions

Booleans:

Represent true by a function that picks the first of two arguments
Represent false by a function that picks the second of two arguments

$\begin{align} & \text{True} = T\ x\ y\rightarrow x\\ & \text{False} = F\ x\ y\rightarrow y\\ \end{align}$

Use SKI (Let $B$ be a Boolean ($T$ or $F$)):

$\begin{align} &T &=& K\\ &F &=& S\ K\\ &\text{not}\ B &=& B\ F\ T\\ &B1\ \text{or}\ B2 &=& B1\ T\ B2\\ &B1\ \text{and}\ B2 &=& B1\ B2\ F\\ \end{align}$

If-Then-Else

Let $B$ be a Boolean ($T$ or $F$)

$\text{if B then X else Y} = B\ X\ Y$

Combinators

swap

Let’s say we want a combinator

$\text{swap}\ x\ y = y\ x$

Use SKI:

$\text{swap}=S\ (K\ (S\ I))\ (S\ (K\ K)\ I)$

Comprehension

Consider a function equation of one variable: $f\ x=E$:

If we apply function $f$ to argument $x$, the result is $E$.

Systematic way:

Start with a function equation using variables that specifies what we want

An abstraction algorithm A(…) maps the right-hand side to a combinator

The key is to eliminate the variables by replacing them with uses of the combinators $S$, $K$, and $I$

Systematic Approach

Writing Combinators: A Systematic Approach

Consider a function equation of one variable: $f\ x = E$
- If we apply function $f$ to argument $x$, the result is $E$.
We want a combinator $A(E, x)$ that implements $f$
- Therefore, $A(E, x)\ x = E$
- And $A(E, x)$ doesn’t use $x$
- We say we abstract $E$ with respect to $x$
Rules:
- $A(x, x) = I$
- $A(E, x) = K\ E$ if $x$ does not appear in $E$
- $A(E1\ E2, x) = S\ A(E1, x)\ A(E2, x)$
Note: $A(…)$ is not a combinator
- It is a (recursively defined) mapping from expressions with variables to combinators.

Swap

Take swap as an example $\text{swap}\ x\ y = y\ x$:

First abstract $y$

$(\text{swap}\ x)\ y=y\ x$

$\begin{aligned} \text{swap}\ x\\ &=A(y\ x, y)\\ &=S\ A(y,y)\ A(x,y)\\ &=S\ I\ (K\ x) \end{aligned}$

Now eliminate $x$ from the result of the previous step:

$\begin{aligned} \text{swap}\\ &=A(S\ I\ (K\ x), x)\\ &=S\ A(S\ I,x)\ A(K\ x, x)\\ &=S\ (K\ (S\ I))\ A(K\ x, x)\\ &=S\ (K\ (S\ I))\ (S\ A(K,x)\ A(x,x))\\ &=S\ (K\ (S\ I))\ (S\ (K\ K)\ A(x,x))\\ &=S\ (K\ (S\ I))(S\ (K\ K)\ I) \end{aligned}$

tedious, huge and hard to read

Improvement

Improvements

We can introduce helper combinators to reduce the size of abstracted expressions.
In $S\ x\ y\ z$, often $z$ is only used in one of $x$ or $y$
- We can avoid copying $z$ and just pass it to the one combinator that uses it.
Define:
- $c1\ x\ y\ z = x\ (y\ z)$ — a version of S where the first argument is constant (doesn’t use z)
- $c2\ x\ y\ z = (x\ z)\ y$ — a version of S where the second argument is constant (doesn’t use z)
Add new cases to the abstraction algorithm for applications that use $c1$ or $c2$ if possible:
- $A(E1\ E2, x) = c1\ E1\ A(E2, x)$ if $x$ does not appear in $E1$
- $A(E1\ E2, x) = c2\ A(E1, x)\ E2$ if $x$ does not appear in $E2$
- $A(E1\ E2, x) = S\ A(E1, x)\ A(E2, x)$ otherwise